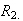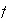 is defined on a closed, bounded region
is defined on a closed, bounded region
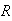 in the xy-plane, then the double integral of
in the xy-plane, then the double integral of
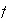 over
over
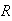 is defined as follows:
is defined as follows:
by Jayne Overgard
Texas A&M University
Definition of a Double Integral
If
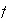 is defined on a closed, bounded region
is defined on a closed, bounded region
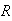 in the xy-plane, then the double integral of
in the xy-plane, then the double integral of
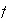 over
over
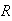 is defined as follows:
is defined as follows:
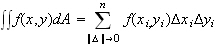
provided the limit exists.
Definition of Volume of a Solid Region
The volume of a solid region that lies above a plane region
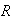 and below the graph of
and below the graph of
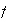 is defined as follows:
is defined as follows:
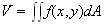
Let
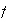 and
and
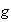 be continuous over a closed, bounded plane region
be continuous over a closed, bounded plane region
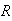 ,
and let
,
and let
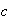 be a constant. Then the following properties hold:
be a constant. Then the following properties hold:
1.
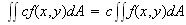
2.
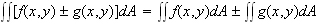
3.
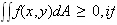
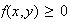
4.
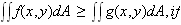

5.
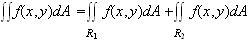
where
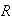 is the union of two nonoverlapping subregions
is the union of two nonoverlapping subregions
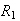 and
and